So erstellen Sie ein Glockenkurvendiagramm in Microsoft Excel

Grafiken und Excel-Diagramme sind eine großartige Möglichkeit, komplexe Datensätze zu visualisieren, und Bell-Kurven bilden da keine Ausnahme. Sie ermöglichen eine einfache Analyse einer Normalverteilung und können problemlos in Excel erstellt werden. Finden wir heraus, wie.

Denken Sie daran, dass der Zweck einer Glockenkurve über die reine Verschönerung der Daten hinausgeht. Es gibt viele Formen der Datenanalyse, die an einem solchen Diagramm durchgeführt werden können und viele Trends und Merkmale des Datensatzes offenlegen. In diesem Leitfaden konzentrieren wir uns jedoch nur auf die Erstellung einer Glockenkurve und nicht auf deren Analyse.

Einführung in eine Normalverteilung

Glockenkurven sind nur zur Visualisierung normalverteilter Datensätze nützlich. Bevor wir uns also mit Glockenkurven befassen, werfen wir einen Blick darauf, was eine Normalverteilung überhaupt bedeutet.

Grundsätzlich kann jeder Datensatz, bei dem die Werte weitgehend um den Mittelwert gruppiert sind, als Normalverteilung (oder Gaußsche Verteilung, wie sie manchmal genannt wird) bezeichnet werden. Die meisten natürlich gesammelten Datensätze sind in der Regel so, von Mitarbeiterleistungszahlen bis hin zu wöchentlichen Verkaufszahlen.

Was ist eine Glockenkurve und warum ist sie nützlich?

Da die Datenpunkte einer Normalverteilung um den Mittelwert gruppiert sind, ist es sinnvoller, die Varianz jedes Datenpunkts vom zentralen Mittelwert zu messen als seinen absoluten Wert. Und wenn man diese Varianzen in Form eines Diagramms darstellt, erhält man eine Glockenkurve.

Dadurch können Sie Ausreißer auf einen Blick erkennen und die relative Leistung der Datenpunkte im Vergleich zum Durchschnitt sehen. Bei Dingen wie Mitarbeiterbeurteilungen und Studentenbewertungen haben Sie so die Möglichkeit, die Leistungsschwache zu unterscheiden.

So erstellen Sie eine Glockenkurve

Im Gegensatz zu vielen anderen einfache Diagramme in Excel können Sie eine Glockenkurve nicht erstellen, indem Sie einfach einen Assistenten für Ihren Datensatz ausführen. Die Daten müssen zunächst etwas vorverarbeitet werden. Folgendes müssen Sie tun:

Beginnen Sie mit der Sortierung der Daten in aufsteigender Reihenfolge. Sie können dies ganz einfach tun, indem Sie die gesamte Spalte auswählen und dann zu Daten>Aufsteigend sortierengehen.

Als nächstes Berechnen Sie den Durchschnittswert (oder Mittelwert) mit der Funktion Average. Da das Ergebnis häufig in Dezimalzahlen vorliegt, empfiehlt es sich, es auch mit der Funktion Roundzu koppeln.
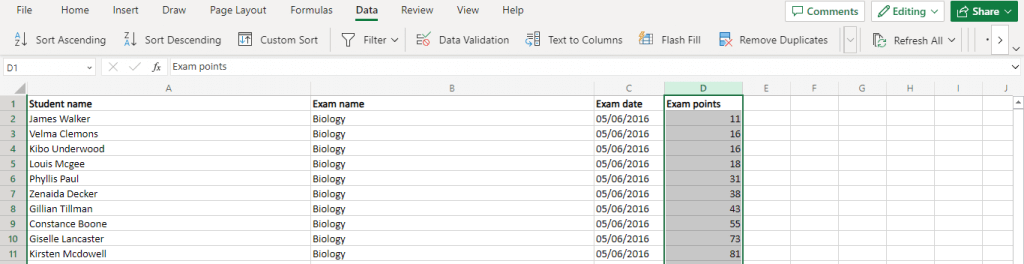
Für unseren Beispieldatensatz sieht die Funktion etwa so aus:
=ROUND (DURCHSCHNITT(D2:D11),0).

Jetzt haben wir zwei Funktionen zur Berechnung der Standardabweichung. STDEV.Swird verwendet, wenn Sie nur eine Stichprobe der Grundgesamtheit haben (normalerweise in der statistischen Forschung), während STDEV.Pverwendet wird, wenn Sie über den vollständigen Datensatz verfügen.

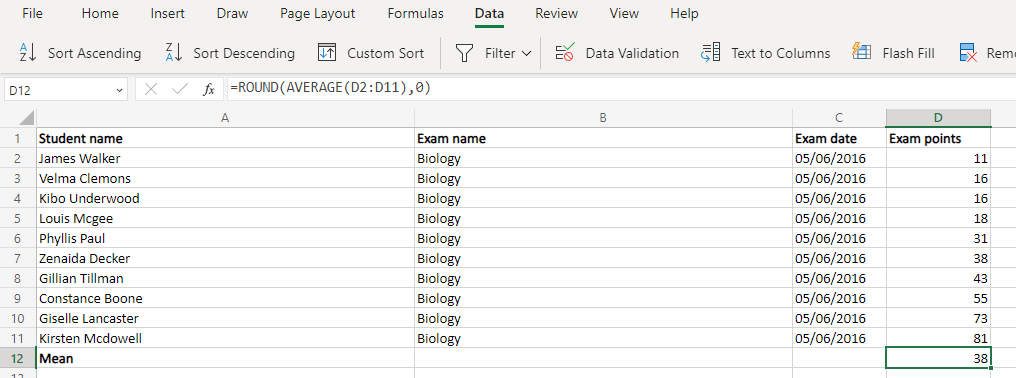
Für die meisten realen Anwendungen (Mitarbeiterbeurteilung, Studentennoten usw.) ist STDEV.P ideal. Auch hier können Sie die Round-Funktion verwenden, um eine ganze Zahl zu erhalten.

=ROUND(STDEV.P(D2:D11),0)

All dies war nur Vorbereitungsarbeit für die tatsächlichen Werte, die wir brauchen – die Normalverteilung. Natürlich verfügt Excel auch hierfür bereits über eine eigene Funktion.

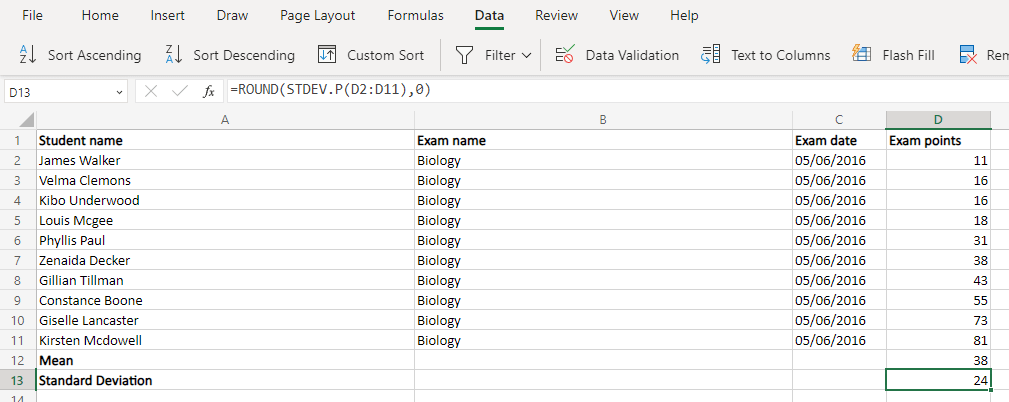
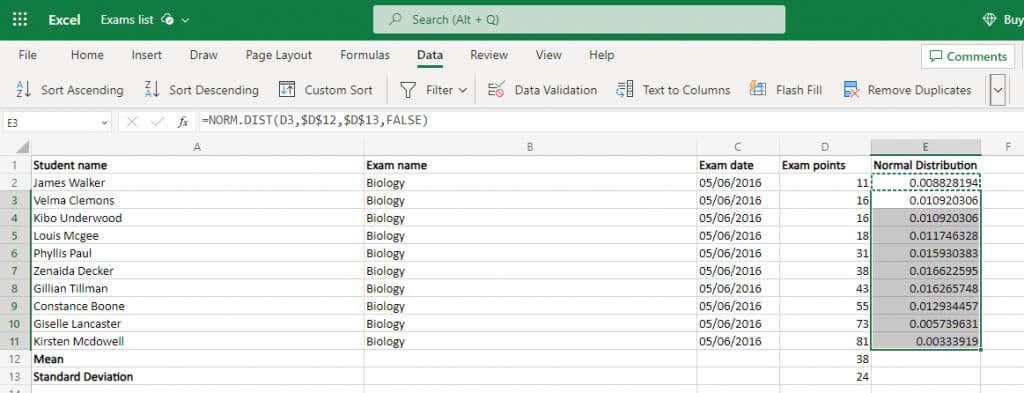
Die Funktion NORM.VERTnimmt vier Argumente entgegen – den Datenpunkt, den Mittelwert, die Standardabweichung und a boolesches Flag, um die kumulative Verteilung zu aktivieren. Den letzten Punkt können wir getrost ignorieren (FALSE eingeben) und haben bereits den Mittelwert und die Abweichung berechnet. Das heißt, wir müssen nur die Zellwerte eingeben und erhalten das Ergebnis.

=NORM.DIST(D2,$D$12,$D$13,FALSE)

Machen Sie es für Geben Sie eine Zelle ein und kopieren Sie dann einfach die Formel in die gesamte Spalte. Excel ändert dann automatisch die Referenzen, um sie an die neuen Positionen anzupassen. Stellen Sie jedoch sicher, dass Sie zuerst die Zellbezüge für den Mittelwert und die Standardabweichung sperren, indem Sie ein $-Symbol verwenden.

Wählen Sie diese Normalverteilung zusammen mit den Originalwerten aus. Die Verteilung bildet die y-Achse, während die ursprünglichen Datenpunkte die x-Achse bilden.

Gehen Sie zum Menü Einfügenund navigieren Sie zu den Streudiagrammen. Wählen Sie die Option Streuung mit glatten Linien.

Wie erstellt man am besten ein Glockenkurvendiagramm in MS Excel?

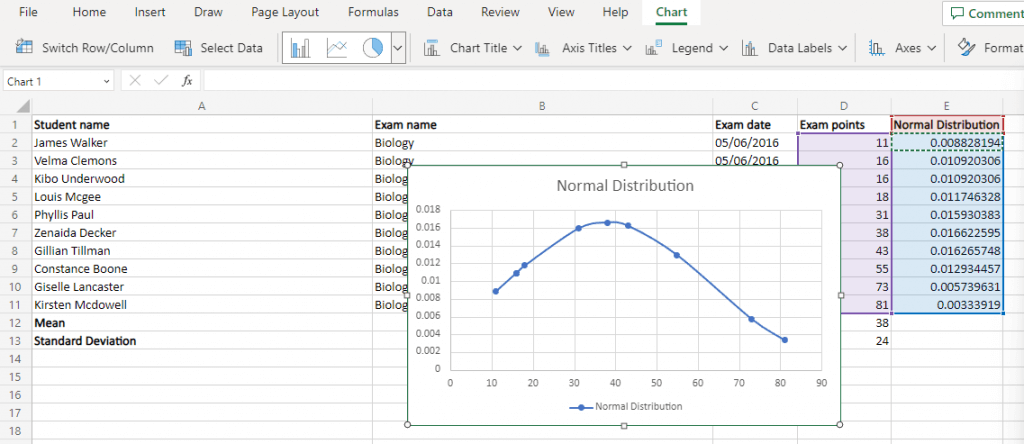
Glockenkurvendiagramme mögen kompliziert erscheinen, sind aber eigentlich ziemlich einfach zu erstellen. Sie benötigen lediglich die Normalverteilungspunkte Ihres Datensatzes.

Bestimmen Sie zunächst den Mittelwert und die Standardabweichung mithilfe integrierter Excel-Formeln. Verwenden Sie diese Werte dann, um die Normalverteilung des gesamten Datensatzes zu berechnen.

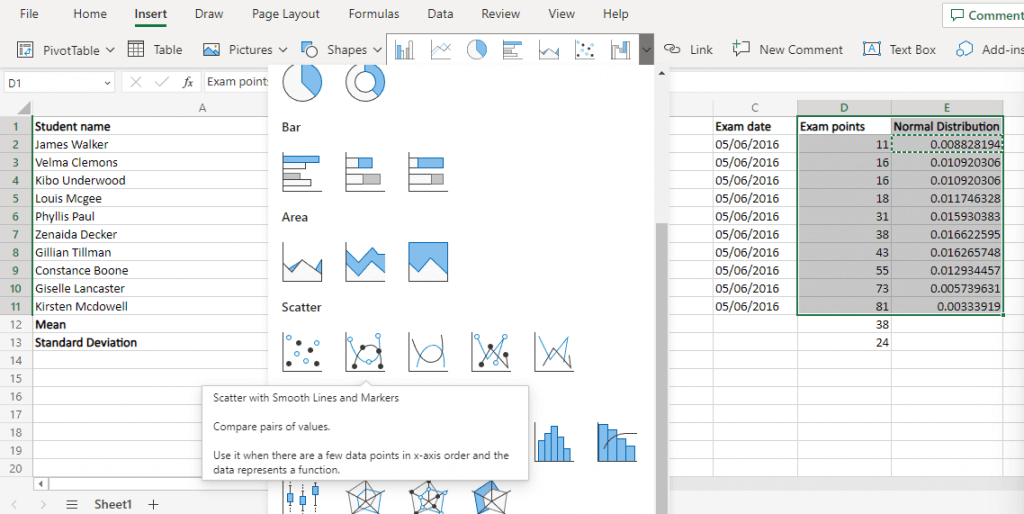
Das Glockenkurvendiagramm ist lediglich ein Streudiagramm mit glatten Linien, das die ursprünglichen Datenpunkte für die x-Achse und die Normalverteilungswerte für die y-Achse verwendet. Wenn Ihr Datensatz normalverteilt war, erhalten Sie in Excel eine glatte Glockenkurve.

Da Sie nun wissen, wie Sie in Excel ein Glockenkurvendiagramm erstellen, schauen Sie sich an, wie Sie ein Gantt-Diagramm erstellen, Wärmekarte oder Wasserfalldiagramm für Ihr Diagramm erstellen nächstes Projekt.

.

Zusammenhängende Posts: